Teknik Rekursi Di Struktur Data & Algoritma

Oct 3, 2024

Rekursi (recursion) adalah sebuah teknik pemograman dimana sebuah function memanggil dirinya sendiri. Walaupun jarang dipakai di pemograman tingkat tinggi seperti aplikasi web, rekursi merupakan fondasi yang penting dan sering dijumpai di persoalan struktur data & algoritma (DS&A). Sebagai contoh, dynamic programming merupakan salah satu bentuk penerapan rekursi dan struktur data tree adalah struktur data yang sering ditelusuri secara rekursif.

Note

Beberapa istilah DS&A terdengar mirip seperti istilah software engineering lainnya tetapi sebenarnya tidak saling berhubungan. Sebagai contoh, dynamic programming pada bahasa pemograman adalah sebuah klasifikasi bahasa pemograman yang tidak memiliki tipe data statis (misalnya Python & JavaScript versus C/C++ & Java). Dynamic programming pada DS&A adalah sebuah teknik dalam menyelesaikan persoalan dimana persoalan dibagi menjadi persoalan yang lebih kecil untuk diproses lewat rekursi. Istilah dynamic disini dipilih karena cara membuatnya yang tidak seperti algoritma konvensional dimana programmer menyelesaikan permasalahan berurutan langkah demi langkah.

Contoh lainnya adalah heap. Pada DS&A, heap adalah struktur data tree dimana nilai dari sebuah node selalu lebih besar (untuk max heap) atau lebih kecil (untuk min heap) dari nilai children-nya. Pada software engineering, heap adalah lokasi memori bebas yang tersedia untuk dipakai oleh kode program (misalnya melalui malloc di C). Heap untuk malloc ini sama sekali tidak berhubungan dengan struktur data tree dan murni hanya kebetulan saja mereka memakai nama yang sama (heap secara literal berarti timbunan atau onggokan).

Salah satu kendala yang saya jumpai saat mempelajari teknik rekursif adalah sulitnya melakukan visualiasi pemanggilan. Untuk itu, saya membuat Visual Recursion dengan harapan supaya saya bisa lebih memahami teknik rekursif.

Rekursi

Pada matematika, contoh klasik rekursi adalah deretan Fibonacci yang didefinisikan sebagai berikut ini:

$$\begin{align} F_0 &= 0,\\ F_1 &= 1,\\ F_n &= F_{n-1} + F_{n-2} \end{align}$$

Walaupun demikian, implementasi-nya di kode program tidak selalu harus lewat rekursi karena function di pemograman memiliki lebih banyak fitur dibandingkan dengan function matematika. Sebagai contoh, ini adalah contoh implementasi function yang mencari angka Fibonacci pada posisi tertentu melalui loop (secara iteratif):

function solve(n: number): number {
    let a = 0;
    if (n === 1) {
        return a;
    }
    let b = 1;
    if (n === 2) {
        return b;
    }
    for (let i=3; i<=n; i++) {
        let sum = a + b;
        a = b;
        b = sum;
    }
    return b;
}

console.log(solve(10));

// OUTPUT:
// 34

Secara umum, kode program versi iteratif memiliki performance yang lebih baik dibandingkan dengan versi rekursif. Walaupun demikian, biasanya versi rekursif lebih mudah dipahami dibandingkan dengan versi iteratif. Contohnya adalah Ackermann function yang didefinisikan seperti berikut ini:

$$A(m,n) = \begin{cases} n + 1 &\text{if }m = 0\\ A(m-1,1) &\text{if }m > 0&\text{ and } n = 0\\ A(m-1, A(m,n-1)) &\text{if }m > 0&\text{ and } n > 0 \end{cases}$$

Function tersebut akan mudah dipahami bisa ditulis melalui pemanggilan rekursif seperti pada contoh kode program berikut ini:

function solve(m: number, n: number): number {
    if (m === 0) {
        return n + 1;
    }
    return solve(m - 1, n === 0 ? 1 : solve(m, n - 1));
}

console.log(solve(2,3));

// OUTPUT:
// 9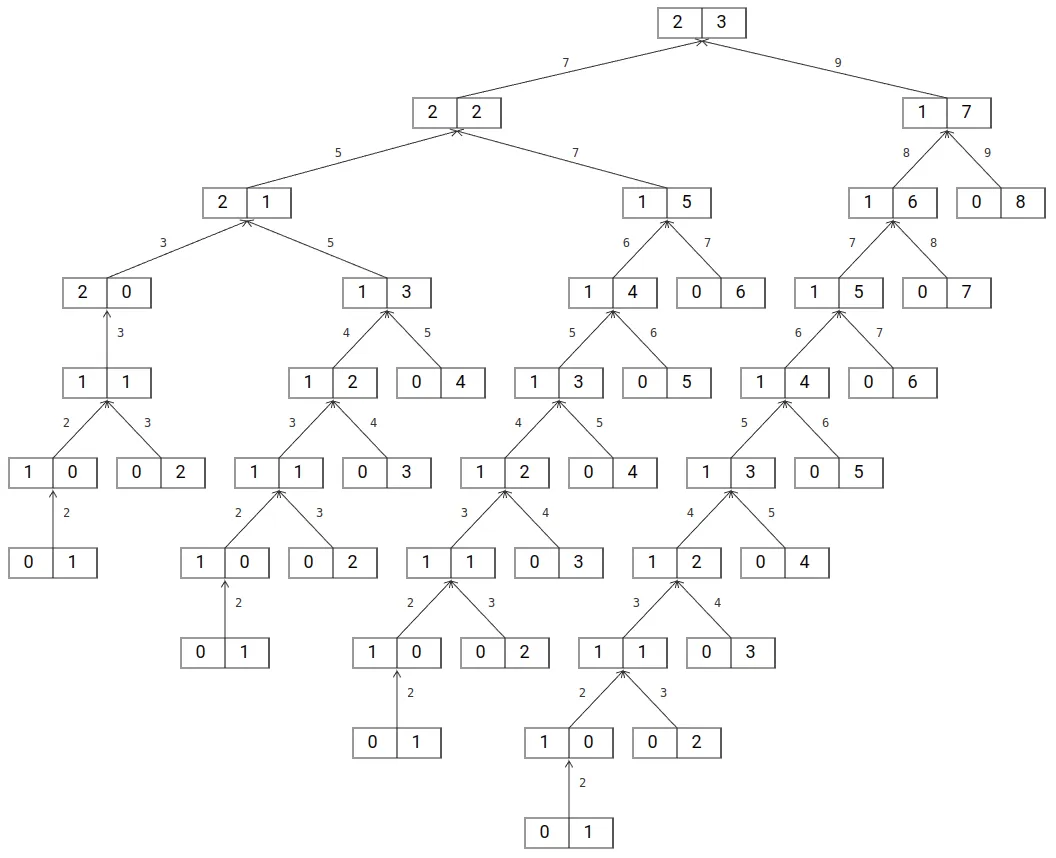

Memoization

Salah satu cara untuk meningkatkan kinerja rekursi adalah dengan menggunakan memoization. Implementasinya lumayan sederhana, cukup simpan hasil kembalian function untuk argumen tertentu sehingga bila nanti ada pemanggilan dengan argumen yang sama, tidak perlu dihitung lagi. Sama seperti bentuk caching lainnya, walaupun kecepatan eksekusi meningkat, memoization akan menambah penggunaan memori.

Sebagai contoh, ini adalah versi kode program yang menghitung Ackermann function yang sudah menggunakan memoization:

const cache = new Map<string, number>();

function solve(m: number, n: number): number {
    const h = `${m};${n}`;
    if (cache.has(h)) {
        return cache.get(h);
    }
    if (m === 0) {
        return n + 1;
    }
    const result = solve(m - 1, n === 0 ? 1 : solve(m, n - 1));
    cache.set(h, result);
    return result;
}

console.log(solve(2,3));

// OUTPUT:
// 9

Bila dilihat dari call tree yang dihasilkan, sekarang terlihat jauh lebih singkat dari versi sebelumnya. Versi tanpa memoization melibatkan 43 kali pemanggilan function. Bandingkan dengan versi memoization yang hanya melibatkan 22 kali pemanggilan function.

Karena Map hanya mendukung sebuah key tunggal, saya menggabungkan m dan n dalam bentuk string. Bila ingin kinerja yang lebih baik lagi, key sebaiknya dalam bentuk sebuah angka. Saya bisa menghasilkan sebuah angka unik dari dua angka yang berbeda dengan menggunakan Cantor pairing function yang didefinisikan seperti berikut ini:

$$\pi(k_1,k_2) = \cfrac{1}{2}(k_1+k_2)(k_1+k_2+1)+k_2$$

dimana $k_1,k_2\in\lbrace0,1,2,3,...\rbrace$.

Versi kode programnya terlihat seperti berikut ini:

const cache = new Map<number, number>();

function pair(m: number, n: number): number {
    return ((m+n)*(m+n+1))/2 + n;
}

function solve(m: number, n: number): number {
    const p = pair(m, n);
    if (cache.has(p)) {
        return cache.get(p);
    }
    if (m === 0) {
        return n + 1;
    }
    const result = solve(m - 1, n === 0 ? 1 : solve(m, n - 1));
    cache.set(p, result);
    return result;
}

console.log(solve(2,3));

// OUTPUT:
// 9

Tail Recursion

Pada saat sebuah function dipanggil, sistem operasi akan menyimpan informasi seperti posisi kembali di sebuah memori sementara yang disebut stack. Bila function tersebut memanggil function lain lagi, informasi posisi saat ini akan ditambahkan ke stack, dan begitu seterusnya. Memori stack ini biasanya terbatas, misalnya area stack secara bawaan adalah 8 MB di Linux dan 1 MB di Windows.

Bila sebuah function memanggil function yang kemudian memanggil function lain dan kemudian memanggil function lain yang kemudian memanggil function lain dan seterusnya hingga area stack menjadi penuh, program akan mengalami kesalahan. Jenis kesalahan seperti ini disebut sebagai stack overflow. Rekursi sangat rentan terhadap kesalahan stack overflow karena banyaknya pemanggil function yang terjadi.

Bila function rekursif yang dipanggil merupakan kode program paling terakhir yang dikerjakan di sebuah function, ia disebut sebagai tail recursion. Salah satu kondisi unik pada tail recursion adalah sebenarnya tidak perlu menggunakan stack untuk mengingat posisi kembali terakhir karena ia bisa langsung kembali ke function sebelum-sebelumnya. Dengan demikian, tail recursion dapat dioptimalisasikan menjadi seperti iterasi tidak akan terjadi stack overflow lagi. Namun, tidak semua compiler atau interpreter mendukung fitur ini. Berdasarkan informasi di artikel Wikipedia, tidak semua browser JavaScript mendukung tail call optimization (terbatas di Safari/WebKit).

Sebagai contoh, berikut ini adalah kode program yang membalikkan string secara rekursif:

function solve(s: string): string {
    if (s.length < 2) return s;
    return solve(s.slice(1)) + s[0];
}

console.log(solve('jocki'));

// OUTPUT:
// ikcoj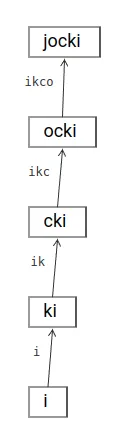

Sementara itu, berikut ini adalah versi yang menggunakan tail recursion:

function solve(s: string, acc?: string): string {
    if (s.length < 2) return acc;
    return solve(s.slice(1), s[0] + (acc ?? ''));
}

console.log(solve('jocki'));

// OUTPUT:
// ikcoj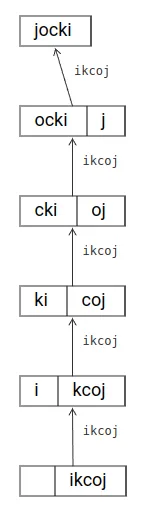

Biarpun sama berakhir dengan return solve() di baris terakhir, kode program pertama tidak menerapkan tail recursion. Hal ini karena return solve(...) + s[0] dimana hasil kembalian pemanggilan rekursif solve(...) perlu ditambahkan lagi dengan s[0]. Ini menunjukkan masih ada yang perlu dilakukan setelah pemanggilan rekursif selesai! Sementara itu, pada program versi kedua, baris terakhir murni return solve(...) tanpa tambahan apa2 sehingga ini adalah tail recursion.

Algoritma Divide and Conquer

Divice and conquer adalah jenis algoritma rekursi yang memecahkan permasalahan menjadi permasalahan kecil untuk diselesaikan, kemudian hasil-nya digabungkan kembali untuk mendapatkan solusi permasalahan tersebut. Salah satu contoh algoritma divide and conquer yang populer adalah quick sort. Berikut ini adalah contoh kode program quick sort:

function solve(arr: number[]): number[] {
    if (arr.length < 2) {
        return arr;
    }
    const pivot = arr[Math.floor(Math.random() * arr.length)];
    const left = [];
    const right = [];
    for (const a of arr) {
        if (a < pivot) {
            left.push(a);
        } else if (a > pivot) {
            right.push(a);
        }
    }
    return [...solve(left), pivot, ...solve(right)];
}

const data = [55,23,44,77,45,90,3,8,2];
console.log(`Unsorted array is `, data);
const sorted = solve(data);
console.log(`Sorted array is `, sorted);

// OUTPUT:
// Unsorted array is   55,23,44,77,45,90,3,8,2
// Sorted array is      2,3,8,23,44,45,55,77,90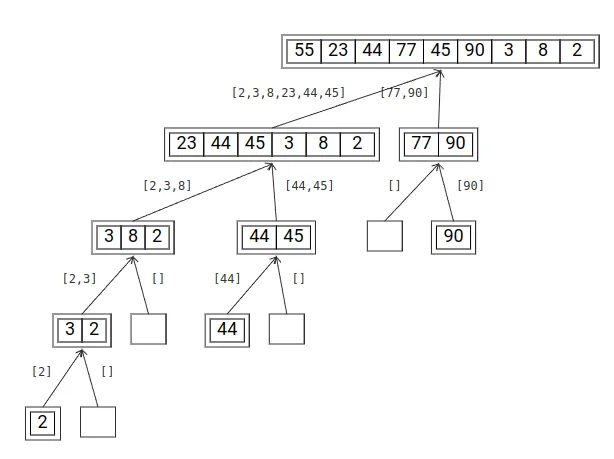

Pada quick sort, terlihat bahwa array yang akan diurutkan dipecah berdasarkan pivot di posisi yang acak. Setelah mencapai ukuran paling kecil, array-array yang kecil ini digabungkan menjadi satu per satu hingga menjadi kembali seperti array awal tetapi kini dengan posisi yang sudah berurut.

Backtracking

Backtracking adalah variasi dari algoritma rekursi yang memungkinkan kode program untuk berhenti dari proses rekursi di saat kondisi sudah tidak valid lagi. Ini adalah bentuk optimalisasi dari pendekatan mencoba brute force semua kombinasi yang ada. Salah satu persoalan yang paling sering dijumpai untuk backtracking adalah N-queen puzzle. Bagaimana cara-nya meletakkan $N$ ratu di papan catur dengan ukuran $NxN$ dimana mereka tidak saling menyerang satu sama lain?

function isSafe(board: number[][], row: number, col: number): boolean {
    for (let i=0; i<col; i++) {
        if (board[row][i] === 1) {
            return false;
        }
    }
    for (let i=row, j=col; i>=0 && j>=0; i--, j--) {
        if (board[i][j]) {
            return false;
        }
    }
    for (let i=row,j=col; j>=0 && i<N; i++,j--) {
        if (board[i][j]) {
            return false;
        }
    }

    return true;
}

function solve(board: number[][], col: number): boolean {
    if (col >= N) {
        return true;
    }
    for (let i=0; i<N; i++) {
        if (isSafe(board, i, col)) {
            board[i][col] = 1;
            if (solve(board, col+1)) {
                return true;
            }
            board[i][col] = 0;
        }
    }
    return false;
}

function createBoard(size: number): number[][] {
    const result = new Array(size);
    for (let i=0; i<size; i++) {
        result[i] = new Array(size).fill(0);
    }
    return result;
}

const N = 4;
const board = createBoard(N);

if (solve(board, 0)) {
    console.log(`The solution for ${N} queens is:\n`);
    for (const row of board) {
        console.log(row);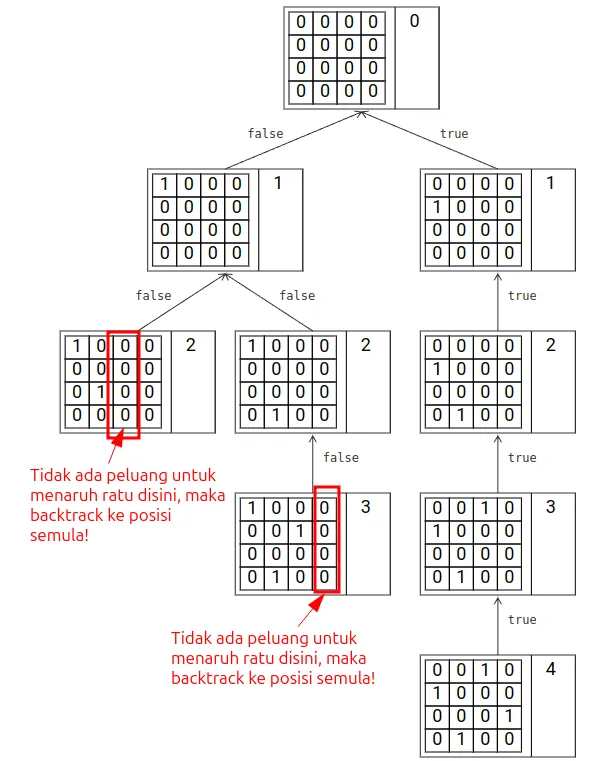
    }
}

Pada kode program di atas, begitu isSafe() mengembalikan false (posisi tidak valid), maka posisi ratu saat ini akan dihapus dan proses rekursi untuk cabang ini tidak akan diteruskan.

Dynamic Programming

Dynamic programming hampir sama seperti divide and conquer yang memecahkan sebuah permasalahan menjadi masalah-masalah kecil. Perbedaannya, pada dynamic programming, permasalahan kecil ini saling berhubungan satu dengan yang lainnya, sementara pada divide and conquer, setiap permasalahan kecil masing-masing berdiri sendiri.

Salah satu contoh dynamic programming adalah longest common subsequence (LCS). LCS dipakai untuk mencari bagian dari string yang sama tetapi tidak perlu berurut. Penerapannya adalah untuk menampilkan diff, revisi seperti di git, dan sebagainya. Definisi LCS secara matematika adalah:

$$LCS(X_i,Y_j)=\begin{cases} \in &\text{if }i = 0\text{ or }j = 0\\ LCS(X_{i-1},Y_{j-1})^\land{x_i} &\text{if }i,j > 0\text{ and }x_i = y_j\\ max\lbrace{LCS(X_i,Y_{j-1}),LCS(X_{i-1},Y_j)}\rbrace &\text{if }i,j > 0\text{ and }x_i\ne{y_j} \end{cases}$$

dimana string yang akan dibandingkan adalah $X = \lparen{x_1},{x_2},\ldots,{x_m}\rparen$ dan $Y = \lparen{y_1},{y_2},\ldots,{y_n}\rparen$. Nilai $X_0,X_1,X_2,\ldots,X_m$ adalah 0, 1, 2 karakter pertama dari $X$ dan seterusnya. Nilai $Y_0,Y_1,Y_2,\ldots,Y_n$ adalah 0, 1, 2 karakter pertama dari $Y$ dan seterusnya. Nilai $\in$ mewakili string kosong. Operator $^\land$ dipakai untuk menggabungkan string.

Dynamic programming bisa dilakukan secara top down (rekursif) ataupun bottom up (iteratif). Teknik bottom up biasanya memakai tabel atau array yang perlu di-isi (disebut juga tabulation). Sebagai contoh, saya bisa membuat tabel untuk rumus matematika di atas dengan kode program seperti berikut ini:

function LCS(X: string, Y: string): number[][] {
    const m = X.length;
    const n = Y.length;
    const C = new Array(m+1);
    for (let i=0; i<m+1; i++) {
        C[i] = new Array(n+1).fill(0);
    }
    for (let i=1; i<=m; i++) {
        for (let j=1; j<=n; j++) {
            if (X[i-1] === Y[j-1]) {
                C[i][j] = C[i-1][j-1]+1;
            } else {
                C[i][j] = Math.max(C[i][j-1], C[i-1][j]);
            }
        }
    }
    return C;
}

const X = "jocki";
const Y = "jokowi";
const C = LCS(X, Y);

Tabel yang dihasilkan untuk "jocki" dan "jokowi" akan terlihat seperti berikut ini:

$$\begin{array}{l|r:r:r:r:r:r:r} & \in & \text{j} & \text{o} & \text{k} & \text{o} & \text{w} & \text{i} \\ \hline \in & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \text{j} & 0 & 1 & 1 & 1 & 1 & 1 & 1 \\ \text{o} & 0 & 1 & 2 & 2 & 2 & 2 & 2 \\ \text{c} & 0 & 2 & 2 & 2 & 2 & 2 & 2 \\ \text{k} & 0 & 2 & 3 & 3 & 3 & 3 & 3 \\ \text{i} & 0 & 1 & 2 & 3 & 3 & 3 & 4 \\ \end{array}$$

Tabel di atas memperlihatkan LCS untuk setiap prefix mulai dari 0 hingga keseluruhan. Sebagai contoh, jumlah LCS joc dan jok adalah 2, jumlah LCS jock dan joko adalah 3. Dan begitu seterusnya. Untuk keseluruhan kata, jumlah LCS jocki dan jokowi yang berada di pojok kanan bawah adalah 4.

Untuk menelusuri setiap perbedaan yang ada di matrix LCS di atas, saya dapat menggunakan teknik rekursi seperti pada kode program berikut ini:

function printDiff(C: number[][], X: string, Y: string, i: number, j: number) {
    if (i >= 0 && j >= 0 && X[i] === Y[j]) {
        printDiff(C, X, Y, i-1, j-1);
    } else if (j > 0 && (i === 0 || C[i][j-1] >= C[i-1][j])) {
        printDiff(C, X, Y, i, j-1);
        console.log("+ " + Y[j]);
    } else if (i > 0 && (j === 0 || C[i][j-1] <= C[i-1][j])) {
        printDiff(C, X, Y, i-1, j);
        console.log("- " + X[i]);
    }
}

const X = "jocki";
const Y = "jokowi";
const C = LCS(X, Y);
printDiff(C, X, Y, X.length, Y.length);

// OUTPUT:
// - c
// + o
// + w

Output di atas memperlihatkan bahwa "jocki" bisa berubah menjadi "jokowi" bila huruf c dihapus dan ow ditambahkan.

Tags:

• Algoritma

Cara Kerja Stateless Authentication Dengan OAuth2 dan JWT

Visual Recursion